The Photoacoustic image reconstruction problem can be viewed as being composed of two parts. The first requires using backpropagation algorithms to reconstruct the absorbed optical energy distribution from the time-dependent photoacoustic signals recorded over an external surface. Currently, we use k-space image reconstruction methods. The advantage of these compared to simple back projection methods is that they provide, in principle, an exact reconstruction (assuming far field detection) resulting in fewer artefacts and, as with the k-space forward propagation models, are computationally efficient through use of the FFT. Although the reconstructed absorbed energy map provides an image of structure, its contrast distribution is a somewhat indirect representation of the tissue optical properties and it is these that directly reflect the tissue composition. This can be seen in figure 1(b) below which shows a “conventionally” reconstructed absorbed energy map of the distribution of absorbers in figure 1(a) The three cylinders can be identified but because the internal light distribution is encoded on the image, the contrast falls off with increasing depth and the lower side of the deepest lying cylinder is barely distinguishable. Thus there remains an additional step in the reconstruction procedure: removing the influence of the internal light distribution in order to recover the distribution of optical coefficients. This has been achieved by iteratively fitting a FE model of light transport to the “conventionally” reconstructed absorbed energy map. Using a straightforward recursive method and simple regularisation techniques, it has been shown that arbitrary distributions of physiologically realistic absorption coefficients in scattering media can be quickly and accurately recovered. As figure 1(c) shows, the technique yields a more accurate contrast distribution (ie one that more closely resembles figure 1(a)) than the conventionally reconstructed image in figure 1(b)). The most obvious advantage is that it aids the visual interpretation of the image. Important as this is, particularly when interpreting images of complex anatomical structures, the real significance is that the image is reconstructed in terms of the absolute absorption coefficient. This means that by obtaining images at multiple wavelengths, the absolute absorption spectra and therefore the concentrations of endogenous chomophores such as oxy and deoxyhemoglobin (for measurement of blood oxygenation) can be determined. It also offers the prospect of quantifying the concentrations of exogeneous chromophores such as those employed in targeted contrast agents for use in photoacoustic molecular and genomic imaging applications.

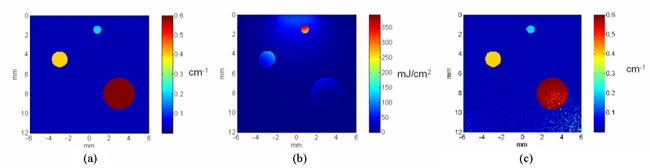
Figure 1 2D quantitative reconstruction of an absorption coefficient distribution. (a) Target absorption distribution comprising 3 absorbing cylinders immersed in scattering media illuminated with a collimated incident on the surface, (b) “conventional” photoacoustic image reconstruction of absorbed energy distribution (includes simulated noise). (c) Reconstructed image of (a) obtained by iteratively fitting a FE model of light transport to (b).

References

• Cox, BT, Arridge, SR, and Beard, PC (2007): Photoacoustic tomography with a limited-aperture planar sensor and reverberant cavity, Inverse Problems 23, S95-S112. Download PDF file
  
• Cox, BT, Arridge, SR, Kostli, KP, and Beard, PC (2006): 2D quantitative photoacoustic image reconstruction of absorption distributions in scattering media using a simple iterative method, Applied Optics 45, 1866-1875. Download PDF file
  
• Cox, BT, Arridge, SR, and Beard, PC (2006): Quantitative photoacoustic image reconstruction for molecular imaging, Proc. SPIE 6086, 60861M. Download PDF file
  
• Cox, BT, Arridge, SR, Köstli, KP, and Beard, PC (2005): Quantitative photoacoustic imaging: fitting a model of light transport to the initial pressure distribution, Proc. SPIE 5697, 49-55. Download PDF file