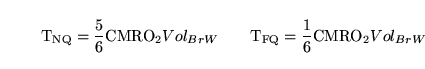

Next: Particular calculations: ion channels
Up: All model parameters
Previous: Metabolic rates and accounting
Subsections
The rate constants for adenylate kinase
We use the rate constants given in (5) to calculate effective rate constants for adenylate kinase. We need effective rate constants because the actual reactants may be free or magnesium bound.
We have from (5) the rate for the reaction as:
![\begin{displaymath}
\ensuremath{\mathrm{k_{fAK}[ADP_f][ADP_{Mg}] - k_{bAK}[ATP_{Mg}][AMP]}}\end{displaymath}](img181.png) |
(55) |
where
![$\ensuremath{\mathrm{[ADP_f]}}$](img182.png) and
and
![$\ensuremath{\mathrm{[ADP_{Mg}]}}$](img183.png) are free and magnesium bound versions of ADP and the same goes for ATP. In our units,
are free and magnesium bound versions of ADP and the same goes for ATP. In our units,
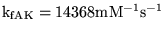 and
and
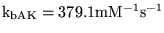 . Also,
. Also,
![$\ensuremath{\mathrm{[ADP_f]}}\simeq 0.0798\ensuremath{\mathrm{[ADP_{tot}]}}$](img186.png) ,
,
![$\ensuremath{\mathrm{[ADP_{Mg}]}}\simeq 0.92\ensuremath{\mathrm{[ADP_{tot}]}}$](img187.png) ,
,
![$\ensuremath{\mathrm{[ATP_{Mg}]}}\simeq \ensuremath{\mathrm{[ATP_{tot}]}}$](img188.png) . So, if we assume that the concentration of magnesium doesn't change, we can write the rate equation:
. So, if we assume that the concentration of magnesium doesn't change, we can write the rate equation:
![\begin{displaymath}
\ensuremath{\mathrm{k_{ADPATP}[ADP_{tot}]^2 - k_{nADPATP}[ATP_{tot}][AMP]}}\end{displaymath}](img189.png) |
(56) |
we get that
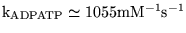 and
and
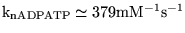 . These are the values that we use. We also have for the effective equilibrium constant:
. These are the values that we use. We also have for the effective equilibrium constant:
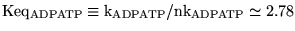 .
.
NAD/NADH concentrations
We have that the average NAD concentration in a cell is:
![\begin{displaymath}
\frac{\ensuremath{\mathrm{[NAD_{cyt}]}}Vol_{cyt} + \ensuremath{\mathrm{[NAD_{im}]}}Vol_{im}}{Vol_{cyt} + Vol_{im}}
\end{displaymath}](img193.png) |
(57) |
In (6) it is stated from work done on the rat heart that the mitochondria possess 72 per cent of cellular NAD content, i.e.
![\begin{displaymath}
0.28\ensuremath{\mathrm{[NAD_{im}]}}Vol_{im} = 0.72\ensuremath{\mathrm{[NAD_{cyt}]}}Vol_{cyt}
\end{displaymath}](img194.png) |
(58) |
Assuming that we know the relative volumes of cytoplasm and mitochondria, and also know the average concentration of NAD in a cell (given in for example (7)) we can calculate the cytoplasmic and mitochondrial concentrations from these two equations.
The rate constants for haemoglobin
In this section we are interested in the equilibria of the four chemical reactions involving haemoglobin, oxygen and protons. Two equilibrium constants -
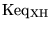 ,
,
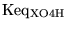 - can be found in the literature, leaving
- can be found in the literature, leaving
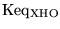 and
and
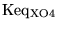 to be determined. We first note that although
to be determined. We first note that although
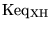 ,
,
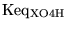 are defined as usual in the literature, the last two -
are defined as usual in the literature, the last two -
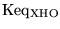 and
and
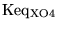 - we define somewhat differents. For completeness we state all the definitions:
- we define somewhat differents. For completeness we state all the definitions:
![\begin{displaymath}
\ensuremath{\mathrm{Keq_{XH}}}= \frac{\ensuremath{\mathrm{[H...
...th{\mathrm{[Hb(H^+)_{n_H}]}}\ensuremath{\mathrm{[O_2]^{2.5}}}}
\end{displaymath}](img199.png) |
(59) |
because we treat the combination of haemoglobin with oxygen as a generalised reaction whose rate is proportion to the
![$\ensuremath{\mathrm{[O_2]^{2.5}}}$](img101.png) . It is more convenient to use these definitions rather than the usual definitions based on the stoichiometry. Despite this difference, some basic algebra (as in (3), Section 16.2) tells us that:
. It is more convenient to use these definitions rather than the usual definitions based on the stoichiometry. Despite this difference, some basic algebra (as in (3), Section 16.2) tells us that:
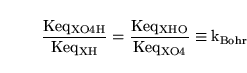 |
(60) |
where this equation defines
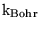 . We now come to the rather tricky question of where to get another equation allowing the determination of all the equilibria.
. We now come to the rather tricky question of where to get another equation allowing the determination of all the equilibria.
We follow (3), Section 16.2. To simplify notation we define
![$\ensuremath{\mathrm{[Hb(O_2)_4]}}= Y$](img202.png) ,
,
![$\ensuremath{\mathrm{[Hb]}}= X$](img203.png) ,
,
![$\ensuremath{\mathrm{[Hb(O_2)_4(H^+)_{n_H}]}}= W$](img204.png) ,
,
![$\ensuremath{\mathrm{[Hb(H^+)_{n_H}]}}= Z$](img205.png) ,
,
![$\ensuremath{\mathrm{[H^+]}}= h$](img206.png) ,
,
![$\ensuremath{\mathrm{[O_2]^{2.5}}}= V$](img207.png) ,
,
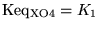 ,
,
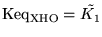 ,
,
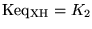 ,
,
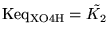 and
and 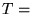 the total haemoglobin in all forms. In this notation, at equilibrium we have the following four equations for the combination of haemoglobin with oxygen and protons:
the total haemoglobin in all forms. In this notation, at equilibrium we have the following four equations for the combination of haemoglobin with oxygen and protons:
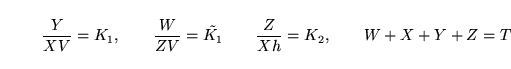 |
(61) |
To obtain a fourth equation we will do the following: First we need to obtain a function describing the total oxygen saturation 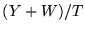 as a function of oxygen tension. Then we can compare this function to empirically obtained functions to set our fourth rate constant. This all takes some algebra.
as a function of oxygen tension. Then we can compare this function to empirically obtained functions to set our fourth rate constant. This all takes some algebra.
We rewrite the equations in terms of the variable
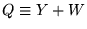 , eliminating
, eliminating 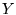 to get:
to get:
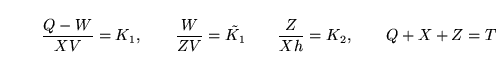 |
(62) |
We substitute for 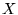 into the last of these to get:
into the last of these to get:
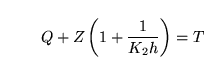 |
(63) |
We solve the first and third equations for 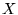 to get:
to get:
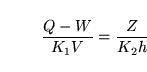 |
(64) |
and solve this for 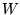 :
:
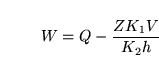 |
(65) |
We combine this with the second equation for 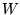 (
(
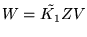 ) to get:
) to get:
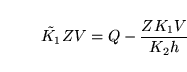 |
(66) |
and rearrange to get:
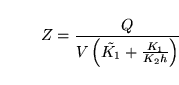 |
(67) |
Finally we substitute back for 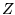 into 63 to get:
into 63 to get:
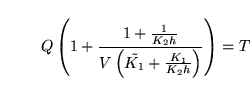 |
(68) |
This can be rearranged to give:
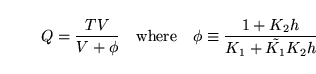 |
(69) |
This equation is important because it is known from empirical investigations of the dissociation curve for haemoglobin at pH 7.4 that half-maximal saturation occurs at oxygen partial pressures of about 26 mmHg. In other words at pH 7.4 the curve:
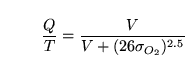 |
(70) |
where 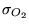 is the solubility of oxygen in blood, reproduces the dissociation curve well. We can use this estimate for
is the solubility of oxygen in blood, reproduces the dissociation curve well. We can use this estimate for  to calculate the final equilibrium constant. Substituting
to calculate the final equilibrium constant. Substituting
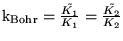 gives:
gives:
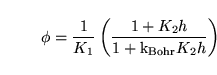 |
(71) |
Setting
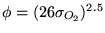 , putting the value for
, putting the value for 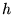 at pH 7.4, and rearranging gives:
at pH 7.4, and rearranging gives:
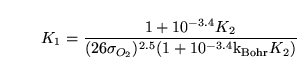 |
(72) |
Or in terms of the original variables:
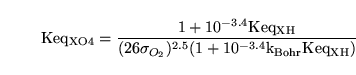 |
(73) |
Thus equations 60 and 73 can be used to determine
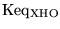 and
and
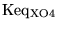 .
.
Finally we mention that the actual rate constants (as opposed to these equilibrium constants) are then calculated using the methodology in section 2.2.1 from equilibrium and half-time data.
Calcium dynamics
Calcium is assumed to be supplied by a process dependent on the membrane potential, and removed by an active mechanism. The total dynamics for calcium are:
![\begin{displaymath}
\ensuremath{\mathrm{\dot{[Ca_{i, j}^{2+}]} = k_{Cain, j} - \...
...t} + \ensuremath{\mathrm{[Ca_{i, j}^{2+}]}}}}}\quad\quad j=1,2
\end{displaymath}](img237.png) |
(74) |
At steady state we therefore have in segment j :
![\begin{displaymath}
\ensuremath{\mathrm{[Ca_{i, j}^{2+}]_n = \frac{k_{Cain, j, n}Km_{Caout}}{Vmax_{Caout, j} - k_{Cain, j, n}}}}\quad\quad j=1,2
\end{displaymath}](img238.png) |
(75) |
Linearising about this steady state value gives us to first order:
![\begin{displaymath}
\dot \delta_j = -\frac{\ensuremath{\mathrm{Vmax_{Caout, j}}}...
...math{\mathrm{Km_{Caout} [Ca_{i, j}^{2+}]_n}}} \quad\quad j=1,2
\end{displaymath}](img239.png) |
(76) |
where 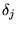 is a small perturbation to
is a small perturbation to
![$\ensuremath{\mathrm{[Ca_{i, j}^{2+}]}}$](img241.png) . From this we derive the relation:
. From this we derive the relation:
![\begin{displaymath}
t_{1/2, \ensuremath{\mathrm{Ca}}} = \ensuremath{\mathrm{\fra...
...out} + [Ca_{i, j}^{2+}]_n)}{Vmax_{Caout, j}}}}\quad\quad j=1,2
\end{displaymath}](img242.png) |
(77) |
Here
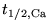 is an approximate half-time for Calcium inflow and outflow which we assume to be the same in each segment. We assume that we can find
is an approximate half-time for Calcium inflow and outflow which we assume to be the same in each segment. We assume that we can find
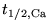 ,
,
![$\ensuremath{\mathrm{[Ca_{i, j}^{2+}]_n}}$](img244.png) and
and
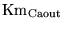 in the literature and equations 75 and 77 to determine
in the literature and equations 75 and 77 to determine
 and
and
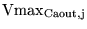 . We define a parameter
. We define a parameter
![$\ensuremath{\mathrm{Km_{Caout, ratio} = Km_{Caout}/[Ca_{i, 1, n}]}}$](img248.png) , and note that if
, and note that if
 is small this implies that the cells' ability to extrude calcium is rapidly reached.
is small this implies that the cells' ability to extrude calcium is rapidly reached.
NO dynamics
The dynamics for NO are very simple:
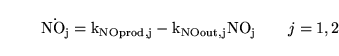 |
(78) |
At equilibrium we expect:
![\begin{displaymath}
\ensuremath{\mathrm{[NO_j]_n = \frac{k_{NOprod, j, n}}{k_{NOout, j}}}}\quad\quad j = 1, 2
\end{displaymath}](img251.png) |
(79) |
By linearising equation 78 we obtain the expression for the halftime:
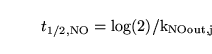 |
(80) |
As with calcium, we currently assume that the halftime is the same in both segments. We treat
![$\ensuremath{\mathrm{[NO_j]_n}}$](img253.png) and
and
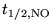 as parameters to be determined from the literature, and use them to determine
as parameters to be determined from the literature, and use them to determine
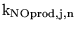 and
and
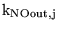 using equations 79 and 80.
using equations 79 and 80.
Myosin phosphorylation and dephosphorylation
We assume that the total quantity of myosin in the cell remains constant at some value
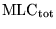 , i.e.
, i.e.
![\begin{displaymath}
\ensuremath{\mathrm{MLC_{tot}}}\equiv \ensuremath{\mathrm{[MLC_{p, j}]}}+ \ensuremath{\mathrm{[MLC_j]}}\end{displaymath}](img258.png) |
(81) |
which we currently assume to be the same in each section. We also define a parameter describing the normal fraction of unphosphorylated myosin heads in each segment:
![\begin{displaymath}
\ensuremath{\mathrm{MLC_{frac, j} \equiv [MLC_j]_n/MLC_{tot}}}\quad\quad j = 1,2
\end{displaymath}](img259.png) |
(82) |
We then treat
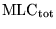 and
and
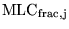 as parameters to be determined from the literature and use equations 81 and 82 to determine
as parameters to be determined from the literature and use equations 81 and 82 to determine
![$\ensuremath{\mathrm{[MLC_j]_n}}$](img261.png) and
and
![$\ensuremath{\mathrm{[MLCp_j]_n}}$](img262.png) .
.
At equilibrium we have:
![\begin{displaymath}
\frac{\ensuremath{\mathrm{[MLC_{p, j}]_n}}}{\ensuremath{\mat...
...\frac{k_{MLCac, j, n}}{k_{MLCinac, j, n}}}}\quad\quad j = 1,2
\end{displaymath}](img263.png) |
(83) |
From this equation we get that:
![\begin{displaymath}
\ensuremath{\mathrm{\frac{[MLC_j]_n}{MLC_{tot} - [MLC_j]_n} = \frac{k_{MLCinac, j, n}}{k_{MLCac, j, n}}}}\quad\quad j = 1,2
\end{displaymath}](img264.png) |
(84) |
i.e.
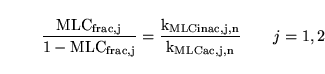 |
(85) |
A linearisation about the fixed point now gives:
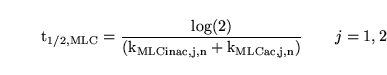 |
(86) |
We now treat
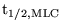 as a parameter to be determined from the literature, and use equations 85 and 86 to determine
as a parameter to be determined from the literature, and use equations 85 and 86 to determine
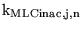 and
and
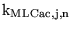 .
.
In section 3 above, we noted that the gross production of
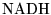 and
and
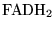 are equal to
are equal to
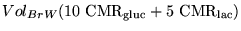 and
and
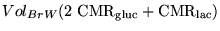 respectively. We also noted that this implies that
respectively. We also noted that this implies that
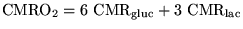 .
.
We can use these data to calculate
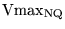 and
and
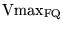 . Let
. Let
 be the turnover rate for oxygen in the equation for the oxidation of
be the turnover rate for oxygen in the equation for the oxidation of
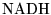 , and
, and
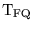 be the turnover rate for oxygen in the equation for the oxidation of
be the turnover rate for oxygen in the equation for the oxidation of
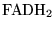 . Then we get the equations:
. Then we get the equations:
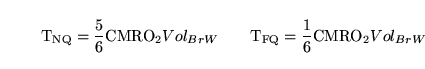 |
(87) |
which can be solved for
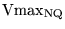 and
and
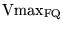 .
.


Next: Particular calculations: ion channels
Up: All model parameters
Previous: Metabolic rates and accounting
Murad Banaji
2004-07-08
![\begin{displaymath}
\ensuremath{\mathrm{k_{fAK}[ADP_f][ADP_{Mg}] - k_{bAK}[ATP_{Mg}][AMP]}}\end{displaymath}](img181.png)
![\begin{displaymath}
\ensuremath{\mathrm{k_{fAK}[ADP_f][ADP_{Mg}] - k_{bAK}[ATP_{Mg}][AMP]}}\end{displaymath}](img181.png)
![\begin{displaymath}
\ensuremath{\mathrm{k_{ADPATP}[ADP_{tot}]^2 - k_{nADPATP}[ATP_{tot}][AMP]}}\end{displaymath}](img189.png)
![\begin{displaymath}
\frac{\ensuremath{\mathrm{[NAD_{cyt}]}}Vol_{cyt} + \ensuremath{\mathrm{[NAD_{im}]}}Vol_{im}}{Vol_{cyt} + Vol_{im}}
\end{displaymath}](img193.png)
![\begin{displaymath}
0.28\ensuremath{\mathrm{[NAD_{im}]}}Vol_{im} = 0.72\ensuremath{\mathrm{[NAD_{cyt}]}}Vol_{cyt}
\end{displaymath}](img194.png)
![\begin{displaymath}
\ensuremath{\mathrm{Keq_{XH}}}= \frac{\ensuremath{\mathrm{[H...
...th{\mathrm{[Hb(H^+)_{n_H}]}}\ensuremath{\mathrm{[O_2]^{2.5}}}}
\end{displaymath}](img199.png)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and ![]() the total haemoglobin in all forms. In this notation, at equilibrium we have the following four equations for the combination of haemoglobin with oxygen and protons:
the total haemoglobin in all forms. In this notation, at equilibrium we have the following four equations for the combination of haemoglobin with oxygen and protons:
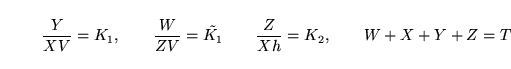
![]() , eliminating
, eliminating ![]() to get:
to get:
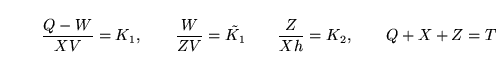
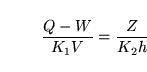
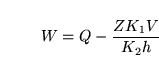
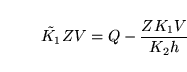
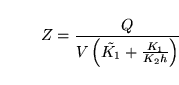
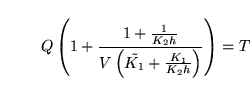
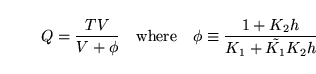
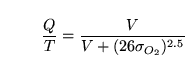
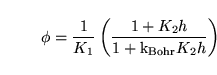
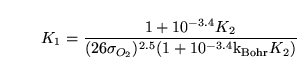
![\begin{displaymath}
\ensuremath{\mathrm{\dot{[Ca_{i, j}^{2+}]} = k_{Cain, j} - \...
...t} + \ensuremath{\mathrm{[Ca_{i, j}^{2+}]}}}}}\quad\quad j=1,2
\end{displaymath}](img237.png)
![\begin{displaymath}
\dot \delta_j = -\frac{\ensuremath{\mathrm{Vmax_{Caout, j}}}...
...math{\mathrm{Km_{Caout} [Ca_{i, j}^{2+}]_n}}} \quad\quad j=1,2
\end{displaymath}](img239.png)
![\begin{displaymath}
\ensuremath{\mathrm{\frac{[MLC_j]_n}{MLC_{tot} - [MLC_j]_n} = \frac{k_{MLCinac, j, n}}{k_{MLCac, j, n}}}}\quad\quad j = 1,2
\end{displaymath}](img264.png)
![]() and
and
![]() . Let
. Let
![]() be the turnover rate for oxygen in the equation for the oxidation of
be the turnover rate for oxygen in the equation for the oxidation of
![]() , and
, and
![]() be the turnover rate for oxygen in the equation for the oxidation of
be the turnover rate for oxygen in the equation for the oxidation of
![]() . Then we get the equations:
. Then we get the equations: