Model outline

Outline of the model

Spatial structure

The basic physical layout of the model is presented in Figure 1. We can see from this figure which compartments are able to communicate with each other. So for example, chemicals in the extracellular space can have a direct effect on vascular smooth muscle, while chemicals in the cellular cytoplasm cannot. The mitochondria can only communicate with rest of the model via the cell cytoplasm.

**Figure 1:** An outline of the physical structure of the model, showing which compartments are in direct contact and can communicate with each other. We consider this the minimum necessary compartmentation to reproduce important effects such as the effect of ischaemia.
$\begin{table}\includegraphics[height = 7.5cm]{modelphysstruct.eps}\end{table}$

For a particular physical structure to qualify as a ``compartment'', the underlying assumption is that it is homogeneous - for example there are no chemical gradients within the compartment (or equivalently, chemical concentrations are well described by some average values). Bearing this in mind, the compartmentation we use is of course a caricature of the considerably more complicated physical structure of the brain. We have chosen it however because we feel that this is the least complicated compartmentation with which we can hope to reproduce the essential effects we are interested in.

A future project it to provide greater discretisation of the model. In this case, the above structure can be seen as a single unit, and a discretised model would consist of many such units interacting only via the extracellular space.

We now explain the meaning of each model compartment, and its role in the model.

Vascular system

The vascular system is the backbone of the model. It is subdivided into the following compartments:

Proximal arteries

This is the first arterial segment containing larger vessels which are able actively to change diameter, and hence resistance, in response to a number of stimuli. Blood flows into these vessels from the systemic circulation, and so input pressure is arterial blood pressure. This compartment is given a resistance based on assumptions about the typical number, length and diameter of the vessels in it. When we refer to pressure in this segment, we mean pressure at the mid-point of the segment.

Distal arteries

This is the second arterial segment containing smaller vessels. Blood flows from the proximal arteries into the distal arteries. These too are able actively to change diameter in response to a number of stimuli. Again an average resistance can be computed based on assumptions about the number, length and diameter of the vessels which make up this segment. As with the proximal compartment, pressure refers to pressure at the midpoint of the segment.

Because they are able actively to change their diameter, the arterial compartments are the effectors of autoregulation. For this reason they play a key role in the model.

Capillaries

These are embedded in the brain parenchyma and assumed to have fixed resistance. They are the site of exchange of chemicals such as oxygen and CO₂ between the blood and the extracellular space. This is their main function in the model - as the site for exchange of chemicals with the rest of the brain tissue.

Cerebral veins and venous sinuses

This section consists of an intracerebral venous section and a venous sinus section. Resistance is assumed constant for the first of these, as it is assumed to be embedded in the brain parenchyma. Venous pressure refers to pressure at the mid-point between the two sections. Venous compliance refers to the compliance at this point, and is inversely dependent on the transmural pressure, with a small constant term added to ensure that the veins collapse at slightly negative transmural pressure.

The venous sinus section has conductance which depends both on transmural pressure and the pressure drop down the vessels - i.e. it behaves as a Starling resistor. Venous sinus pressure refers to pressure at the end of this segment, as does the compliance which is constant.

Extracerebral components

At the ends of the vascular system and essentially outside the model, we have the systemic arteries and the systemic veins. Central arterial and venous pressures are parameters in the model. Arterial chemical concentrations are also important parameters.

Processes in the circulatory system

There are a number of important biophysical processes occurring including:

the relationships between pressure, resistance and flow rate in all the compartments
the way that passive and active responses of the arterial vessels combine to give the total response of these vessels (central to the control of blood flow)

There is also some essential biochemistry in this compartment which we model:

the interaction of oxygen, haemoglobin and protons in the blood
the removal of carbon dioxide

Extracellular space

This space contains the CSF and the extracellular fluid, but the space is not further subdivided in the model. There is assumed to be a slow flow of CSF through the space. As it flows it carries with it all associated chemicals, and is thus responsible for the drainage of chemicals which have no other way of exiting the extracellular space.

The extracellular space also contains chemicals such as adenosine and protons which can have a feedback effect on vascular smooth muscle via activating receptors or ion channels on the smooth muscle surface.

Role of the extracellular space

The extracellular space is important as the intermediary between the vascular system and the tissue itself. Chemicals such as glucose, oxygen, and CO₂ pass through as they travel between blood and brain. Being in contact with vascular smooth muscle cells, it also mediates a number of feedback effects on these cells. Intracranial pressure refers to pressure in the extracellular space. Various pathologies can be represented via the blockage of CSF drainage pathways leading to increases in intracranial pressure.

Vascular smooth muscle (VSM)

There are two VSM compartments which control the diameter of the proximal and distal arterial segments respectively. They contain calcium, nitric oxide (NO) and muscle proteins. The membrane potential of the smooth muscle cells, which is taken to be determined by the conductivity to potassium and the potassium concentration, determines the rate of inflow of calcium into the cells. Various stimuli such as shear stress determine the level of NO in the cells. Calcium and NO determine the level of phosphorylation of myosin light chains, and this in turn determines the level of tension and hence the arterial diameter.

Effects of stimuli on vascular smooth muscle

Vascular smooth muscle is the key effector of autoregulation. It responds to physical stimuli like transmural pressure and shear stress and to chemical stimuli like adenosine, protons, and nitric oxide. The resultant alterations in smooth muscle tension change the diameter of the resistance vessels and hence blood flow. Changes in blood flow in turn give rise to changes in the rate of delivery and removal of various metabolic substrates and products. An outline of how smooth muscle tone is controlled in the model is shown in Figure 2. Stimuli in the model act primarily via two overlapping pathways - alteration of VSM membrane potential leading to the inflow of calcium into the cell, and stimulation/inhibition of the production of nitric oxide. These pathways overlap because nitric oxide itself has two effects on vascular smooth muscle, one direct and one via alterations in potassium channel conductivity. Stimuli affect membrane potential mostly by altering the conductivity of potassium channels in the VSM membrane (these are the main determinant of membrane potential), although the extracellular potassium concentration also has a direct effect on membrane potential. These pathways are summarised in the figure below.

**Figure 2:** A caricature of the control of smooth muscle in the model. The dashed line represents the action of extracellular potassium which has a direct effect on membrane potential (as well as an indirect effect via altering the conductivity of inward rectifier potassium channels).
$\begin{table}\includegraphics[height = 4.5cm]{smoothmuscle.eps}\end{table}$

Action of calcium and nitric oxide on muscle proteins

Thus levels of calcium and NO are the key determinants of VSM tone. In Figure 3 we show the direct effects of calcium and NO on smooth muscle in the model. Calcium and NO concentrations are maintained by the balance of (stimulus-dependent) inflow/production and outflow/degradation processes. The levels of calcium and NO serve to determine (via nonlinear relationships) the rate of myosin phosphorylation and dephosphorylation respectively. NO also has a further indirect action via altering potassium channel conductivity and hence calcium influx, which is not shown in the diagram.

Figure 3: The opposing actions of calcium and nitric oxide on smooth muscle proteins.

$\includegraphics[height = 6.5cm]{canoaction.eps}$

Calcium and nitric oxide (NO) have opposing actions on smooth muscle proteins in the model. Calcium increases the rate of myosin light chain phosphorylation (conversion of MLC to MLC_p ) while NO increases the rate of myosin light chain dephosphorylation. It is the proportion of phosphorylated myosin which is taken to determine the level of force generated by vascular smooth muscle.

Segmental heterogeneity

In general, in the model we allow for the possibility that the different VSM segments might respond to the same stimuli in different ways. These differences might for example represent different levels of expression of certain ion channels. It is often stated for example that the smaller arteries and arterioles respond more to metabolic stimuli while the larger vessels respond directly to pressure changes. Thus parameters associated with each segment are allowed to take distinct values.

Cellular cytoplasm

The cellular compartments are currently not differentiated into neurons and glia, although it is known that these cells perform different functions. The cytoplasmic compartment is the cite of glycolysis and lactate production. The active maintenance of ion gradients across the cell walls accounts for a large fraction of energy use of the brain, and is probably also involved in coupling brain electrical activity to local metabolism. This compartment is also the site of a number of other reactions such as the reactions catalysed by creatine kinase and adenylate kinase.

Role of the cytoplasmic compartment

This compartment is important for a number of reasons. Glycolysis taking place within it provides some of the cellular energy via a (small) production of ATP and NADH, but more importantly provides pyruvate for entry into the TCA cycle. It is the site of production of lactic acid, an important mediator of the effect of hypoxia. Further the cytoplasm contains the majority of volume in the model and changes which involve the build-up/outflow of various substances take effect at time-scales related to this volume.

Mitochondria

Mitochondria have been included in the model primarily because there was the concern that any less differentiated approach might not be able to reproduce sufficiently well the effects of altered stimuli/pathology on metabolism.

Pyruvate, the end product of glycolysis enters the mitochondrial compartment, and then enters the TCA cycle. Apart from the TCA cycle, also occurring in this compartment are electron transport and oxidative phosphorylation. The NAD/NADH ratio and the mitochodrial membrane potential are important variables connected with this compartment. This is the site where a lack of oxygen takes effect, leading indirectly (via changes in the NAD/NADH ratio) to increases in lactate production and a number of other effects.

Role of the mitochondria

The mitochondria are important primarily as metabolic powerhouses. This is important because a large part of the model concerns the production and use of energy in the form of ATP, and the consequences of a mismatch between supply and demand. The majority of ATP production takes place in the mitochondria.

A summary of mitochodrial dynamics is shown in Figure 4.The figure can be followed from right to left.

**Figure 4:** A summary of mitochondrial dynamics in the model.
$\begin{table}\includegraphics[height = 8cm]{mitoproc.eps}\end{table}$

Metabolic control

Some of the principal pathways of metabolic control in the model are shown in Figure 5. Thus for example changes in metabolic demand affect the rate of glycolysis and of ATPase by altering the levels of adenosine phosphates, while the TCA cycle and electron transport communicate primarily via changes in the NAD/NADH ratio. The proton motive force (primarily determined by the membrane potential) serves to couple the rates of electron transport and ADP phosphorylation although this coupling is imperfect due to the proton leak. Because glycolysis is treated as an irreversible process in the model, a lack of oxygen, brings mitochondrial metabolism to a halt, but has an activating effect on glycolysis via increased levels of AMP.

**Figure 5:** Some key pathways of metabolic control in the model.
$\begin{table}\includegraphics[height = 4.5cm]{metabcontrol.eps}\end{table}$

Metabolic control in the model is not meant to represent the true complexity of pathways of control in metabolism. Currently a number of activating and inhibiting pathways are excluded.

Energy production and use

ATP is the main source of energy in the model. Intermediates such as NADH are important inasmuch as they can ultimately produce ATP. Pathways leading to enegy production are presented in Figure 6.

Figure 6: The metabolic fates of various substrates in the model.

$\includegraphics[height = 10cm]{accounting.eps}$

Numbers next to the arrows represent the numbers of product molecule produced per substrate molecule: These do not necessarily correspond to the stoichiometries of any reaction, as the substrate molecule may be involved in other reactions. N1_H is the number of protons pumped out of the mitochondrial matrix during the oxidation of two molecules of NADH. N2_H is the number of protons pumped out during the oxidation of two molecules of FADH₂ . z is the number of molecules of ATP produced for each proton that re-enters the mitochondrion.

Regarding ATP use, the basic model assumption is that there are two ATP-consuming processes: ionic homeostasis via Na⁺, K⁺ -ATPase, and a lumped process representing all other pathways. The consequences of insuffient ATP production are seen in decreased flux through these two pathways. Ionic gradients are crucial to the brain's function, and the loss of these gradients (i.e. cellular depolarisation) is the model equivalent to death.

Transport processes

Transport between compartments is central to the model. It is important partly because it determines time constants - the rate of transport of substances between intracellular space and extracellular space are an important determinant of the average length of time it takes for metabolic alterations to have an effect on vascular smooth muscle. It is also important within the circulatory system - for example reduced blood flow leads to reduced supply of oxygen, with a large number of metabolic side-effects. A number of chemicals are produced at one site and needed at another, and the rate of transport can, at least in some circumstances be a limiting factor.

Further, the maintenance of chemical gradients via transport processes is central to the physiology in question. The maintenance of ionic gradients between the cells and the extracellular space via an active transport process is key. And during oxidative phosphorylation, energy is stored in the proton gradient created.

Convective transport

There are two convective processes in the model: the flow of blood through the vascular system, and the drainage of CSF. In both cases, all chemicals dissolved in the fluid are transported convectively with it. The convective transport of oxygen (bound to haemoglobin) and carbon dioxide are probably the two most important examples of convective transport in the model.

Diffusion and carrier mediated transport

Substances such as dissolved gases traverse the blood brain barrier, and also cell and mitochondrial membranes by diffusion. The gradients in both oxygen and CO₂ tension between compartments are testimony to the fact that these processes cannot be ignored, and at very low oxygen tensions it is the diffusion rate of oxygen which becomes limiting.

Carrier mediated transport also occurs throughout the model. Glucose crosses the blood-brain barrier by a carrier-mediated process. Substances like lactate, pyruvate, phosphate, ATP-ADP, NAD/NADH are all involved in symport or antiport between mitochondria and cytoplasm, or cytoplasm and extracellular space in carrier-mediated processes. During hypoxia lactate builds up in the brain tissue because its transporters (monocarboxylate transporters) saturate.

Active transport

There are a number of instances of active transport explicitly or implicitly treated. The two key ones at the heart of the model are:

Na⁺ - K⁺ exchange across the cell membrane. This process, by which the cell's integrity is maintained is a major energy consumer in the model. (All other energy consumption is treated as a single lumped process.)
The maintenance of mitochondrial membrane potential via proton transport. As NADH and FADH₂ are oxidised, protons are pumped out of the mitochondrial matrix. Currently we assume that mitochondrial membrane potential is generated entirely via this process.

Sources

Our work draws on a large amount of existing physiological and modelling work. Here we mention a few of the most important. There is nothing to beat Edvinsson et al. Edvinsson and Krause (2002) for a broad sweep of all that concerns the cerebral circulation. An older but still useful introduction to the relevant physiology is Mraovitch and Sercombe (1996). Aubert and Costalat Aubert and Costalat (2002) provide the inspiration for this kind of integrated modelling. The model of vascular biophysics is taken almost intact from the model in Ursino and Lodi (1998), and other work by Ursino has provided inspiration on many occasions. Sources on vascular smooth muscle are numerous, but luckily there are some good books and review articles such as Bárány (1996), Nelson and Quayle (1995), Faraci and Heistad (1998), Davis and Hill (1999). A basic understanding of much relevant metabolic biochemistry has come from Garrett and Grisham (1995) and Bhagavan (2002). Siesjö (1978) cannot be omitted in any discussion on brain energy metabolism. Insights into how we might begin to model the relevant biochemisty come from the modelling work in Cortassa et al. (2003) and Korzeniewski (2001) amongst many others. Finally, our bible for translating physiology into mathematics is Keener and Sneyd (1998).

The computational and logical structure of the model is modular, allowing for independent testing of its components. This conceptual framework is outlined in Banaji and Baigent (forthcoming).

Summary

Although in a state of evolution, components of the model have been tested against physiological data with promising results. In addition, data from clinical studies has been input into the model as a whole with qualitative agreement between model simulations and observed behaviour.

Bibliography

A. Aubert and R. Costalat.: A model of the coupling between brain electrical activity, metabolism, and hemodynamics: Application to the interpretation of functional neuroimaging.
NeuroImage, 17 (3): 1162-1181, 2002.
M. Banaji and S. Baigent.: A flexible, iterative, approach to physiological modelling.
In R. Paton and D. Leishman, editors, Multidisciplinary approaches to theory in medicine. Elsevier, forthcoming.
M. Bárány, editor.: Biochemistry of Smooth Muscle Contraction.
Academic Press, 1996.
N.V. Bhagavan.: Medical Biochemistry.
Harcourt/Academic Press, 2002.
S. Cortassa, M. A. Aon, E. Marbán, R. L. Winslow, and B. O'Rourke.: An integrated model of cardiac mitochondrial energy metabolism and calcium dynamics.
Biophys J, 84: 2734-2755, 2003.
M. J. Davis and M. A. Hill.: Signalling mechanisms underlying the vascular myogenic response.
Physiol Rev, 79 (2): 387-423, 1999.
L. Edvinsson and D. N. Krause, editors.: Cerebral Bood Flow and Metabolism.
Lippincott Williams and Wilkins, 2002.
F. M. Faraci and D. D. Heistad.: Regulation of cerebral circulation: Role of endothelium and potassium channels.
Physiol Rev, 78 (1): 53-97, 1998.
R. H. Garrett and C. M. Grisham, editors.: Biochemistry.
Saunders College Publishing, 1995.
J. Keener and J. Sneyd.: Mathematical Physiology, volume 8 of Interdisciplinary Applied Mathematics.
Springer, 1998.
B. Korzeniewski.: Theoretical studies on the regulation of oxidative phosphorylation in intact tissues.
Biochim et Biophys Acta - Bioenergetics, 1504 (1): 31-45, 2001.
S. Mraovitch and R. Sercombe, editors.: Neurophysiological basis of cerebral blood flow control: An introduction.
John Libbey, 1996.
M. T. Nelson and J. M. Quayle.: Physiological roles and properties of potassium channels in arterial smooth muscle.
Am J Physiol Cell Physiol, 268 (4): C799-C822, 1995.
B. K. Siesjö.: Brain energy metabolism.
Wiley, 1978.
M. Ursino and C. A. Lodi.: Interaction among autoregulation, 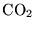$\ensuremath{\mathrm{CO_2}}$ reactivity, and intracranial pressure: a mathematical model.
Am J Physiol Heart Circ Physiol, 274 (5): H1715-H1728, 1998.

Up: Index of documentation

Murad Banaji
2004-07-08